Целые числа
Tilda Publishing
Делимость целых чисел
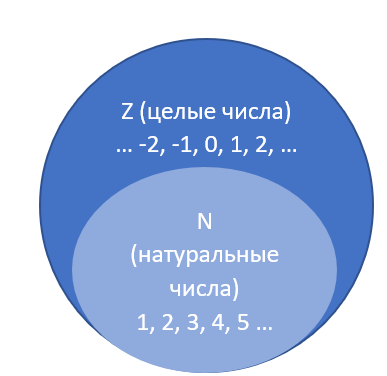
На множестве натуральных чисел 1, 2, 3, 4, 5, ... задаются известные арифметические операции: сложение, умножение, а также вычитание и деление. Вычитание и деление могут быть выполнены во множестве натуральных чисел, если их результатом являются натуральные числа. Кроме того, любые два числа можно сравнить между собой по величине, т.е. установить одно из отношений меньше, равно, больше. Можно расширить совокупность натуральных чисел до множества целых чисел
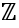
: добавить
и отрицательные целые числа -1, -2, -3, -4, -5, ... . Тогда множество целых чисел будет замкнуто
0
еще и относительно операции вычитания, т.е. для любых чисел a и b, принадлежащих
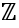
, их разность a - b также является
целым числом.
Частное от деления одного целого числа на другое может уже не быть целым числом.
Говорят, что целое число a делит целое число b, если найдется целое число c такое, что b=a∙c. И пишут
Говорят, что целое число a делит целое число b, если найдется целое число c такое, что b=a∙c. И пишут
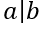
.
Число a называется делителем числа b.
Делитель a называется собственным делителем числа b, если
Делитель a называется собственным делителем числа b, если
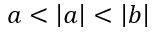
, и несобственным в противном случае.
Например,
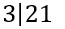
; число 3 делит число 21, так как 21=3∙7. При этом число 3 является собственным делителем числа 21.
Положительное, целое число
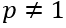
называется простым, если оно не имеет собственных делителей, и составным в
противном случае.
Например:
2, 3, 5, 7, 11, 13, 17, 19, 23 и т.д. - простые числа;
4, 6, 8, 0, -2, 9, 10, -3,-4 и т.д. - составные числа.
Например:
2, 3, 5, 7, 11, 13, 17, 19, 23 и т.д. - простые числа;
4, 6, 8, 0, -2, 9, 10, -3,-4 и т.д. - составные числа.
Tilda Publishing
Свойства делимости

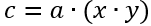
,
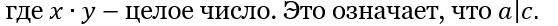
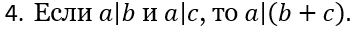
Tilda Publishing
Свойства собственного делителя
1.Положительный наименьший собственный делитель составного числа n не превосходит
Доказательство.
Пусть положительный наименьший собственный делитель составного числа n равен p, тогда n=p∙q, где q - собственный делитель n не меньший p. Получаем
2.Положительный наименьший собственный делитель составного числа n есть простое число.
Доказательство.
Пусть p положительный наименьший собственный делитель n не простое число. Значит, оно имеет собственный делитель q:1<q<p<n, при этом
Доказательство.
Пусть положительный наименьший собственный делитель составного числа n равен p, тогда n=p∙q, где q - собственный делитель n не меньший p. Получаем
2.Положительный наименьший собственный делитель составного числа n есть простое число.
Доказательство.
Пусть p положительный наименьший собственный делитель n не простое число. Значит, оно имеет собственный делитель q:1<q<p<n, при этом
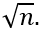
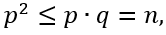
таким образом,
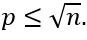
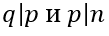
. По свойству транзитивности получаем, что
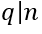
. Таким образом, q - собственный
делитель n меньший p - противоречивое.
Рассмотрим пример на применение данных свойств: найти наименьший собственный делитель числа 287.
Для этого нужно проверить все простые числа от 2 до
Рассмотрим пример на применение данных свойств: найти наименьший собственный делитель числа 287.
Для этого нужно проверить все простые числа от 2 до
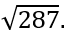
Или от 2 до 13.
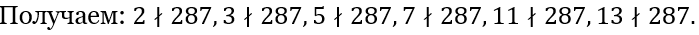
Таким образом, данное число является простым.
Tilda Publishing
Основная теорема арифметики
Теорема. Любое целое число (n>1) может быть представлено в виде произведения простых чисел и при этом единственным образом с точностью до порядка сомножителей.
Доказательство.
1) пусть n>1 - простое число. Тогда запишем n = p , и теорема верна.
2) Пусть n>1 - составное. Обозначим через p положительный наименьший собственный делитель числа n. По свойствам
p - является простым числом и n = p ∙n .
Если n - простое, обозначим его p и запишем n = p ∙ p .Если n - составное, то поступим с ним также как с n, выделив положительный наименьший собственный делитель. Получим n = p ∙ p ∙ n ..И так далее. Такой процесс конечен, то есть на некотором шаге число n будет обязательно простым. Таким образом, получили следующее разложение n = p ∙ p ∙ p ∙. . .∙ p и доказали теорему.
Разложение
1) пусть n>1 - простое число. Тогда запишем n = p , и теорема верна.
2) Пусть n>1 - составное. Обозначим через p положительный наименьший собственный делитель числа n. По свойствам
p - является простым числом и n = p ∙n .
Если n - простое, обозначим его p и запишем n = p ∙ p .Если n - составное, то поступим с ним также как с n, выделив положительный наименьший собственный делитель. Получим n = p ∙ p ∙ n ..И так далее. Такой процесс конечен, то есть на некотором шаге число n будет обязательно простым. Таким образом, получили следующее разложение n = p ∙ p ∙ p ∙. . .∙ p и доказали теорему.
Разложение
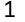
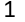
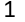
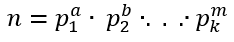
, где p все различные простые, a, b, . . . ,m - натуральные, называется каноническим
разложением числа n.
Например, найдем каноническое разложение числа m = 1620.
m = 1620 = 2 ∙ 810 = 2 ∙ 2 ∙405 = 2 ∙ 2 ∙ 3 ∙ 135 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 45 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 15 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 5.
Например, найдем каноническое разложение числа m = 1620.
m = 1620 = 2 ∙ 810 = 2 ∙ 2 ∙405 = 2 ∙ 2 ∙ 3 ∙ 135 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 45 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 15 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 3 ∙ 3 ∙ 5.
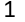
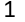
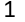
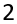
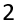
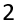
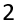
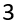
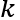
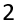
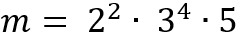
.
Tilda Publishing
Деление с остатком
Теорема. Для данного целого отличного от нуля числа b, всякое целое число a единственным образом представимо в виде a = b ∙ q + r, где
Доказательство.
Ясно, что одно представление числа равенством a = b ∙ q + r мы получим, если возьмем b ∙ q равным наибольшему кратному числа b, не превосходящему a.
Тогда, очевидно,
Пусть a = b ∙ q + r и a = b ∙ q + r - два таких представления. Значит
Здесь
Доказательство.
Ясно, что одно представление числа равенством a = b ∙ q + r мы получим, если возьмем b ∙ q равным наибольшему кратному числа b, не превосходящему a.
Тогда, очевидно,
Пусть a = b ∙ q + r и a = b ∙ q + r - два таких представления. Значит
Здесь
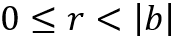
.
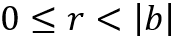
.
Докажем единственность такого представления.
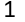
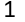
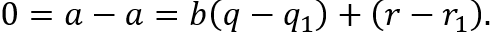
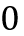
делится на b;
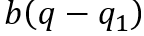
делится на b, следовательно
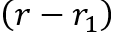
обязано делится на b.
Так как
равно нулю, т.е. два таких представления совпадают. Теорема доказана.
Число q называется неполным частным, а число r - остатком от деления a на b.
Рассмотрим примеры:
Если a = 9, b = 4; 9 = 4 ∙ 2 +1, q = 2, r = 1.
Если a = -9, b = 4; -9 = 4 ∙ (-3) +3, q = -3, r = 3.
Если a = -11, b = 3; -11 = 3 ∙ (-4) +1, q = -4, r = 1.
равно нулю, т.е. два таких представления совпадают. Теорема доказана.
Число q называется неполным частным, а число r - остатком от деления a на b.
Рассмотрим примеры:
Если a = 9, b = 4; 9 = 4 ∙ 2 +1, q = 2, r = 1.
Если a = -9, b = 4; -9 = 4 ∙ (-3) +3, q = -3, r = 3.
Если a = -11, b = 3; -11 = 3 ∙ (-4) +1, q = -4, r = 1.
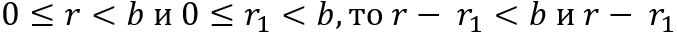
делится на b, значит
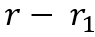
равно нулю, а значит и
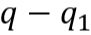
Tilda Publishing
НОД и НОК. Их свойства
Пусть a и b - целые положительные числа. Целое число d называется наибольшим общим делителем чисел a и b, если d делит одновременно a и b и каждый другой общий делитель a и b делит d. Обозначается НОД (a, b).
Известно, что НОД двух чисел - единственный.
Говорят, что два целых числа a и b взаимно простые, если их единственными общими делителями являются единицы
Известно, что НОД двух чисел - единственный.
Говорят, что два целых числа a и b взаимно простые, если их единственными общими делителями являются единицы
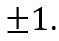
Действительно, написанное выше равенство показывает, что всякий общий делитель чисел a и b делит также и c и, следовательно, является общим делителем чисел b и c. Обратно, то же равенство показывает, что всякий общий делитель чисел b и c делит a и, следовательно, является общим делителем чисел a и b. Таким образом общие делители чисел a и b суть те же, что и общие делители чисел b и c; в частности, должны совпадать и наибольшие из этих делителей, т.е. НОД(a,b)=НОД(b,c).
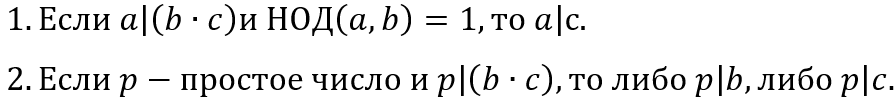
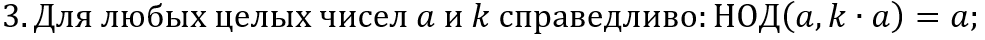
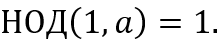
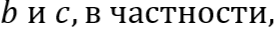
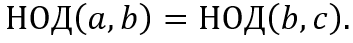
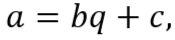
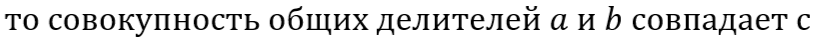
5.
Если для целых чисел a и b существуют целые x и y такие, что
то НОД(a,b) = 1.
то НОД(a,b) = 1.
ax + by = 1,
Для разыскания общего наибольшего делителя применяется алгоритм Евклида. Также, перейдя по ссылке, советуем обратить внимание на раздел "Простые и составные числа", в котором приводится доказательство, что наибольшего простого числа не существует. Здесь рассмотрим теорему.
Для составления таблицы простых чисел древний грек Эратосфен придумал процедуру, которая получила название "решето Эратосфена".
Для составления таблицы простых чисел древний грек Эратосфен придумал процедуру, которая получила название "решето Эратосфена".
Пусть a и b - целые положительные числа. Целое число m называется наименьшим общим кратным чисел a и b, если m делится одновременно на a и b и каждое другое общее кратное a и b делится на m. Обозначается НОК [a, b].
Известно, что НОК двух чисел - единственно.
Свойства:
Известно, что НОК двух чисел - единственно.
Свойства:
- Если НОД (a, b) = 1, то НОК [a, b] = a ∙ b.
- a ∙ b = НОД(a, b) ∙ НОК [a, b].
По всем вопросам свяжитесь с нами любым удобным способом:
E-mail: hello@company.com
Телефон: +123 466 567 78
Соцсети: Facebook | Instagram | Youtube
E-mail: hello@company.com
Телефон: +123 466 567 78
Соцсети: Facebook | Instagram | Youtube
