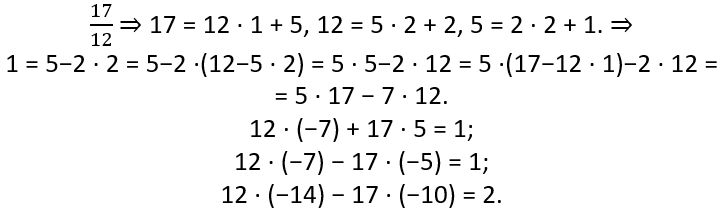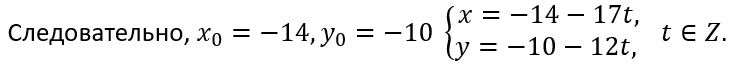Диофантовы уравнения первого порядка с двумя неизвестными
Tilda Publishing
Историческая справка
Термин диофантовы уравнения берет свое начало от имени выдающегося греческого математика Диофанта из Александрии.
Диофант искусно решал алгебраические и теоретико-числовые задачи, не давая общих методов решения. Диофант строил алгебру на арифметике, при этом со своим языком и символикой. Его можно считать автором первого алгебраического языка. До нашего времени, дошла примерно половина (6 из 13 книг) его главного труда - математического трактата «Арифметика» (250-275гг).
Поскольку большинство задач в этой книге предусматривают решения в целых числах, то для анализа подобного рода проблем стал применяться термин диофантов.
Сегодня диофантов анализ - это обширная, сложная область теории чисел, которой посвящена многочисленная научная литература.
Диофант искусно решал алгебраические и теоретико-числовые задачи, не давая общих методов решения. Диофант строил алгебру на арифметике, при этом со своим языком и символикой. Его можно считать автором первого алгебраического языка. До нашего времени, дошла примерно половина (6 из 13 книг) его главного труда - математического трактата «Арифметика» (250-275гг).
Поскольку большинство задач в этой книге предусматривают решения в целых числах, то для анализа подобного рода проблем стал применяться термин диофантов.
Сегодня диофантов анализ - это обширная, сложная область теории чисел, которой посвящена многочисленная научная литература.

Диофант
III в. н.э.
III в. н.э.
Tilda Publishing
Диофантовы уравнения первого порядка с двумя неизвестными
Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида
где m, n, k, x, y∈ Z, k≠0.
Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида
где m, n, x, y ∈ Z.
Теорема 1 Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Например, уравнение 34x - 17y = 3 в целых числах неразрешимо, так как 3 не делится нацело на 17.
Теорема 2 Если коэффициенты m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Теорема 3 Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений. Все эти решения описываются формулами
где
Теорема 4 Если пары чисел
уравнения (2).
Теорема 5 Если m и n взаимно простые числа, то всякое решение уравнения (2) имеет вид
Далее рассмотрим методы решений неоднородных диофантовых уравнений первого порядка.
где m, n, k, x, y∈ Z, k≠0.
Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида
где m, n, x, y ∈ Z.
Теорема 1 Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.
Например, уравнение 34x - 17y = 3 в целых числах неразрешимо, так как 3 не делится нацело на 17.
Теорема 2 Если коэффициенты m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.
Теорема 3 Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений. Все эти решения описываются формулами
где
Теорема 4 Если пары чисел
уравнения (2).
Теорема 5 Если m и n взаимно простые числа, то всякое решение уравнения (2) имеет вид
Далее рассмотрим методы решений неоднородных диофантовых уравнений первого порядка.
mx + ny = k
(1)
mx + ny = 0
(2)
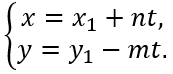
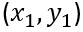
-какое-либо решение уравнения (1), t ∈ Z.
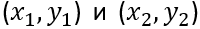
решения уравнения (1), то пара чисел
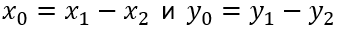
-решения
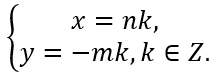
Tilda Publishing
Метод рассмотрения остатков от деления
Этот способ удобно применять, если хотя бы один из коэффициентов m, n невелик по модулю. Пусть это будет, например, m. Перепишем уравнение mx + ny = k в виде
Левая часть уравнения (3) делится нацело на m. Значит, должна делиться нацело на m и правая часть данного уравнения.
Рассматривая все возможные остатки l от деления y на m, l=0,1,…,m - 1, получаем, что при одном значении l из указанного промежутка будет делиться на m и правая часть. Поскольку число m невелико по модулю, то перебор вариантов будет тоже невелик.
Левая часть уравнения (3) делится нацело на m. Значит, должна делиться нацело на m и правая часть данного уравнения.
Рассматривая все возможные остатки l от деления y на m, l=0,1,…,m - 1, получаем, что при одном значении l из указанного промежутка будет делиться на m и правая часть. Поскольку число m невелико по модулю, то перебор вариантов будет тоже невелик.
mx = k - ny
(3)
Пример. Решить уравнение 3x - 4y = 1 в целых числах.
Перепишем уравнение в виде 3x = 4y + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая:
1.Если y = 3m, где m∈ Z, то 4y +1 = 12m + 1 не делится на 3.
2.Если y = 3m + 1, то 4y + 1 = 4(3m + 1) +1 = 12m + 5 не делиться на 3.
3.Если y = 3m + 2, то 4y + 1 = 4(3m + 2) + 1=12m + 9 делится на 3, поэтому 3x = 12m + 9 ⇒ x = 4m + 3, откуда следует
где произвольное m ∈ Z.
Перепишем уравнение в виде 3x = 4y + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая:
1.Если y = 3m, где m∈ Z, то 4y +1 = 12m + 1 не делится на 3.
2.Если y = 3m + 1, то 4y + 1 = 4(3m + 1) +1 = 12m + 5 не делиться на 3.
3.Если y = 3m + 2, то 4y + 1 = 4(3m + 2) + 1=12m + 9 делится на 3, поэтому 3x = 12m + 9 ⇒ x = 4m + 3, откуда следует
где произвольное m ∈ Z.
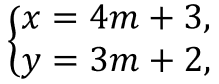
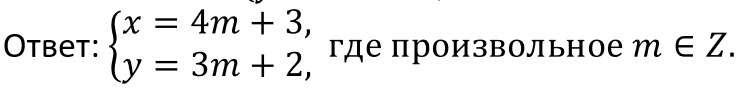
Tilda Publishing
Решение диофантовых уравнений с помощью алгоритма Евклида
Для нахождения наибольшего общего делителя двух целых неотрицательных чисел используют алгоритм Евклида.
Решим диофантово уравнение с помощью алгоритма Евклида.
Пример. Решить уравнение 12x - 17y = 2.
12x - 17y = 2, (12, -17, 2), следовательно, это диофантово уравнение, (12, -17)=1. Данное уравнение разрешимо в целых числах.
Найдем выражение числа 1 через a и b, a = 12, b = -17, но мы будем рассматривать |b|, так как y ∈ Z.
Ответ: (-14 -17t, -10-12t), k ∈ Z.
Решим диофантово уравнение с помощью алгоритма Евклида.
Пример. Решить уравнение 12x - 17y = 2.
12x - 17y = 2, (12, -17, 2), следовательно, это диофантово уравнение, (12, -17)=1. Данное уравнение разрешимо в целых числах.
Найдем выражение числа 1 через a и b, a = 12, b = -17, но мы будем рассматривать |b|, так как y ∈ Z.
Ответ: (-14 -17t, -10-12t), k ∈ Z.